De forma não convencional as crianças recorrem a contagens e operações para resolver pequenos problemas do cotidiano. A escola de educação infantil pode contribuir decisivamente para a aproximação da criança com os conhecimentos matemáticos construídos socialmente

Ainda que não freqüentem nenhuma escola as crianças participam de uma série de situações envolvendo conhecimentos sobre a série numérica oral e seu uso em situações de enumeração, assim como aprendem sobre escritas numéricas em diferentes contextos – ao brincar com um telefone e dizer uma sucessão de números, ao pedir uma determinada quantidade de biscoitos, quando um adulto lhe pergunta quantos anos tem, etc.
“A notação numérica aparece diante das crianças como um dado da realidade.”1
Por um lado, abrir as portas da escola para os conhecimentos matemáticos que as crianças já possuem é uma condição necessária para o trabalho com essa área. Por outro, isto não esgota a sua finalidade. Não se ensina matemática só para que as crianças adquiram conhecimentos úteis para o seu dia-a-dia, mas sim para que se apropriem de uma forma própria de pensar e de fazer, construída culturalmente.
“A escola é sem dúvida a instituição responsável por favorecer que as crianças articulem sua experiência extra-escolar com as questões que se pretende que aprendam; esta articulação não é espontânea, não pode ficar sob a responsabilidade das crianças.”2

Crianças com a ajuda da professora ordenam os valores dos pacotes
Pensar sobre o sistema de numeração
Graças às investigações didáticas, em particular às pesquisas de Delia Lerner e Patricia Sadovsky, hoje sabemos que é a partir do uso dos números, da análise e da reflexão sobre o sistema de numeração que a criança constrói conhecimentos sobre a numeração escrita. As crianças entre 2 e 3 anos, na maioria das vezes, dependem das ações dos adultos para atribuir significados às palavras que indicam números e às escritas numéricas.
Essas aprendizagens variam de acordo com as situações das quais participam. É necessário, portanto, criar nas instituições de Educação Infantil as condições didáticas que propiciem diversos momentos em que as crianças aprendam que os números possuem distintas funções. Por exemplo, quando a professora marca o dia do aniversário de cada um no calendário ou conta a quantidade de crianças para saber quantas folhas serão necessárias distribuir, ao cantar canções que possibilitam a memorização de parte da série numérica, quando inclui materiais com números nas suas brincadeiras (telefone, panfleto de supermercado com preços), etc., o Centro de Educação Infantil está contribuindo para que a criança construa paulatinamente conhecimentos matemáticos.
As crianças entre 4 e 6 anos, em geral, como já alcançaram maior autonomia, podem participar simultaneamente de situações envolvendo o funcionamento dos números em diferentes tipos de problemas e contextos e enfrentar problemas que lhes permitam avançar em seus conhecimentos sobre a série numérica e explorar suas regularidades.
“A análise das regularidades da numeração escrita é uma fonte insubstituível de progresso na compreensão das leis do sistema por parte das crianças.”
Pretendendo socializar as atualizadas pesquisas sobre a didática da Matemática, a Associação das Mulheres pela Educação (AME), localizada em Osasco, São Paulo, promoveu o curso A Aprendizagem e o Ensino da Matemática na Educação Infantil, que tinha como objetivo auxiliar a planejar e analisar propostas de ensino envolvendo números e sistema de numeração.
Dentre as propostas desenvolvidas pelas participantes durante o curso, uma atividade e projeto foram bem interessantes, e aproveito para compartilhar nesta revista.
Quanto custa cada saco de balas?
A professora Gláucia Fischer Vicente, após ler o artigo de Delia Lerner e Patricia Sadovsky e analisar as atividades sugeridas, decidiu propor para o seu grupo de crianças uma lojinha de balas em que elas pudessem, ao organizá-la, comparar e ordenar escritas numéricas.
A seguir, seu relato: A proposta era que as crianças fizessem, com as balas iguais entre si, pacotes que tivessem quantidades diferentes (5, 8,12,15, 20 balas). Os preços desses pacotes seriam (em centavos) com os seguintes valores: 0,45; 0,10; 0,40; 0,60; 0,25; 0,85. Elas teriam que decidir qual o preço de cada tipo de pacote e anotar.
A seguir, seria proposto que, em pequenos grupos, comparassem suas anotações com seus colegas e que, em caso de divergências, argumentassem a favor ou contra as diferentes anotações. Finalmente, se discutiria com todo o grupo para estabelecer acordos. Organizei a turma, distribui o material e lancei a proposta sem muita explicação.
Apenas falei o necessário para aquele momento: “Vocês têm aí cinco saquinhos, e cada um com um certo número de balas. Então contem quantas há em cada saquinho, depois observem os valores que estão anotados na lousa e decidam entre vocês o preço de cada saquinho.”
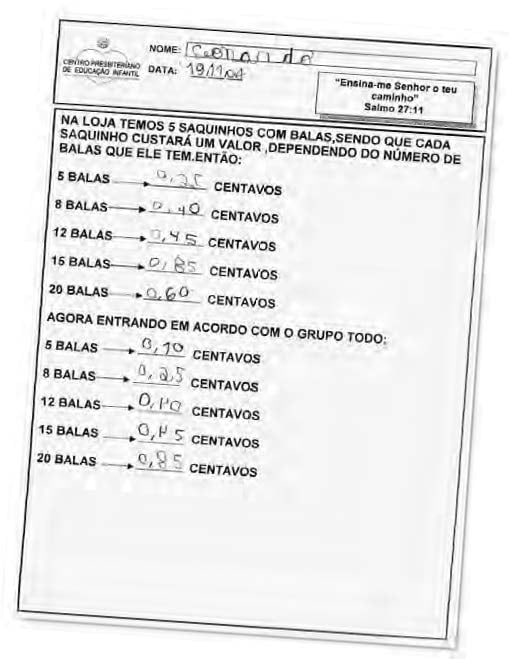
Fichas com a ordem dos valores dos saquinhos de balas
Esta foi a hora do falatório, pois todos os grupos estavam em ação ao mesmo tempo. Algumas crianças davam sua opinião, lutavam por ela e justificavam o porquê do valor atribuído a cada saquinho. Outras observavam ou simplesmente concordavam com o que os colegas decidiam. Não fui capaz de anotar todas as falas dos alunos, a aula estava muito empolgante.
Na hora da socialização com toda a turma, pude conhecer mais claramente os critérios utilizados pelas crianças para decidir o valor de cada saquinho. Comecei a perguntar:
Profa: Quantas balas há em cada saquinho?
Crianças: Tem um com 5, outro com 8, com 12, com 15 e com 20.
Profa: Ok!
Profa: Qual o saquinho que tem a maior quantidade de balas?
(Matheus): O de 20.
Profa: Certo.
Profa: Qual preço deve custar este saquinho?
(Léo e Matheus): 0,85.
Profa: Por quê?
Crianças: Onde tem mais balas custa mais caro!
Profa: Ok! E todos concordam?
Crianças: Concordam.
Profa: Quanto deve custar o saquinho com 5 balas?
Crianças: Essa foi fácil! 0,10!
Profa: Por quê?
(Léo): Porque é o saquinho que tem menos bala.
A partir dessa discussão as crianças foram colocando os outros valores em ordem crescente considerando: maior número de balas, maior preço, menor número de balas, menor preço. Terminamos a atividade com a turma louca de vontade de chupar balas. Foi uma delícia essa atividade de negociar valores e comparar números.
Um projeto: o livro dos recordes
A professora Fabiane Rodrigues se interessou por um projeto envolvendo ordenação e comparação de escritas numéricas, analisado durante o curso, e considerou que ele poderia fazer sentido para seus alunos. Ela havia observado que, em suas conversas, as crianças faziam comparações principalmente ligadas aos atributos físicos:
- Quem tem o cabelo maior?
- Quem tem o pé maior?
- Quem é o mais alto da sala?
Propôs para o grupo a confecção de um livro de recordes em que as crianças precisariam relacionar cada situação a sua informação numérica. Em roda, fizemos um levantamento sobre o que eram recordes. A maioria das crianças não tinha idéia do que isto significava, por isso organizei um cartaz com algumas reportagens sobre o assunto. Li algumas para elas e expliquei que recorde era quando alguém ou alguma coisa era mais ou menos do que as outras. Ex.: o maior prédio do mundo, a menor bicicleta, a pessoa que tem mais tatuagens, etc.
Num outro dia, propus para as crianças organizarem um livro de recordes, onde iríamos colocar diversas informações númericas nas quais os valores superassem os demais. As crianças fizeram uma lista de itens que gostariam de pesquisar:
- A pessoa mais alta
- O maior pé
- O cabelo mais comprido
- Quem tem mais animais
- A pessoa mais velha
- A pessoa mais pesada
- Quem tem mais filhos
Pesquisar, ordenar e comparar
Para começar, propus que descobrissem quem era a criança mais alta da sala. Antes mesmo de iniciarmos a medição, elas começaram a comparar suas alturas encostando-se umas nas outras. Medi as crianças com a fita métrica e elas anotaram sua altura em pedaços de papel. Em seguida, dividi-as em pequenos grupos e pedi que descobrissem quem era a mais alta do seu grupo3.
No início, ao comparar os números, as crianças olhavam o primeiro e o último algarismo, dizendo ser maior o número que começava ou terminava pelo algarismo maior. Ao comparar as alturas, deram-se conta de que os números eram muito parecidos (1,19; 1,20; 1,25). Então passaram a consultar a tabela numérica4 ou a fita métrica, relacionando a contagem oral com as escritas numéricas, concluindo que o número que vem depois é maior.

Crianças consultam tabela numérica
Quando cada grupo já havia concluído a atividade, passamos para a roda, com a finalidade de socializarmos as descobertas e compararmos os números, e então, saber quem era o mais alto da sala. Quando as crianças descobriram quem era o mais alto da sala (Ricardo Jr.: 1,30 m), dei a elas um outro desafio: identificar a pessoa mais alta de toda a creche, incluindo os adultos.
Para isso, elas saíram divididas em grupos, com uma lista contendo todos os nomes das funcionárias (cada grupo tinha que entrevistar três funcionárias), para descobrirem a altura de cada uma. Com a pesquisa pronta, novamente tiveram que ordenar os números, descobrir a maior altura pesquisada em cada grupo e socializar na roda, e assim descobrir quem era a pessoa mais alta da creche (Rose: 1,77 m).
Conseguida essa informação – devidamente anotada em cartazes que ficavam em exposição no mural –, as crianças tiveram que encontrar alguém que fosse mais alto do que a Rose, e para isso levaram um questionário para ser preenchido junto aos familiares.
Com as pesquisas em mãos, fizemos todo o processo de ordenação para descobrirmos quem era a pessoa mais alta de todas. Primeiro, descobrimos que o mais alto de todos era o José, avô do Júnior, com 1,92 m. Mas como as crianças poderiam continuar pesquisando, pouco depois a Mariana trouxe a informação de que o Kiko do KLB (grupo musical) tinha 2,02 m, ou seja, era mais alto. Algumas semanas, depois li para eles uma reportagem sobre as Olimpíadas e descobrimos que o jogador de vôlei do Brasil, o Rodrigão, media 2,04 m. Então, substituímos o Kiko pelo Rodrigão.
Sistematizando os conhecimentos
Durante todo o projeto eu ia ajudando a solucionar dúvidas das crianças ao usar a tabela numérica, na contagem oral, para saber qual número vem antes ou depois, etc. Conseguimos sistematizar alguns conhecimentos importantes para o grupo:
- Quando a gente conta, o número menor vem primeiro, o número que vem depois é maior.
- Quando o número tem mais números ele é maior.
- Quando o número tem a mesma quantidade de números, tem que olhar o primeiro para saber qual é o maior.
- Se o primeiro número for igual, olhamos o segundo para saber qual é o maior.
Esse projeto rendeu muitas informações para as crianças sobre a ordem dos números e regularidades do nosso sistema de numeração. Tenho certeza de que elas se aproximaram um pouco mais da compreensão do complexo sistema posicional.
Os pais também vibraram e se envolveram com esse projeto. A cada nova pesquisa queriam saber quem havia conseguido o “mais” de todos, e procuravam achar outro maior, incentivando seus filhos a levarem a nova informação para a creche.
Vantagens desse tipo de proposta
“Por que propor atividades centradas na comparação? Quando os números são representados através do sistema decimal posicional, a relação de ordem adquire uma especificidade vinculada à ordenação do sistema. É justamente esta especificidade que se tenta mobilizar a partir das situações de comparação que são propostas às crianças.”
As crianças puderam colocar em jogo suas idéias sobre o sistema de numeração que, muitas vezes, não coincidem com os procedimentos convencionais. Tiveram a oportunidade de formular e comunicar seus procedimentos, confrontá-los com os dos colegas, considerando diferentes resoluções e afirmações. Argumentaram e procuraram validar seu ponto de vista, aceitar erros, corrigir tentativas frustradas e estabelecer alguns acordos.
A principal dificuldade para ensinar e aprender sobre essa área do conhecimento consiste na maneira como se concebe a Matemática. É comum, para evitar erros, os professores controlarem a situação, muitas vezes induzindo as crianças à resposta correta.

Página do livro “Os Mais Mais”
Se quisermos que as crianças “façam Matemática”, tomando decisões, agindo como produtoras de conhecimento e não apenas executoras de instruções, precisamos abrir mão desse controle.
Ao propor que os alunos usem seus conhecimentos numa ampla variedade de problemas cuja resolução ainda não lhes foi ensinada, que utilizem diversas estratégias para resolvê-lo, que provem, que se equivoquem, que revisem, que disponham de meios para poder determinar se um procedimento é válido ou não, estamos proporcionando outro modo de relacionar-se com a Matemática.
Assumir esse enfoque que propõe que as crianças reflitam sobre o objeto de conhecimento em toda sua complexidade, significa, necessariamente, aceitar respostas diferentes das convencionais, considerar a provisoriedade do conhecimento e o que as crianças não sabem como algo a ser conquistado por elas.
(Priscila Monteiro, formadora do Instituto Avisa Lá)
1 D. Lerner e P. Sadovsky, em Didática da Matemática, org. C. Parra e I. Saiz. Ed. Artmed.
2 Municipalidad de la Ciudad de Buenos Aires – Actualización Curricular, documento de trabajo no 2. E.G.B. Primer Ciclo. www.buenosaires.gov.ar/educacion/docentes/planeamiento/docum/matematica.php.
3Para organizar os grupos de trabalho Fabiane considerou os saberes de cada um de seus alunos, formando grupos em que os conhecimentos eram próximos.
4Na parede da sala Fabiane colocou uma tabela com números de 1 a 100, que as crianças consultam com desenvoltura. A tabela foi organizada de dez em dez para que, ao consultá-la, as crianças pudessem refletir e utilizar as regularidades do sistema de numeração.
Planejamento da atividade
- Enviar uma pesquisa para ser feita em casa, na qual as crianças devem descobrir alguém que seja mais alto do que a Rose, que mede 1,77 m.
- Dividir a turma em grupos de quatro crianças cada.
- Anotar a resposta da pesquisa em um papel menor (nome e altura) para facilitar a ordenação, já que na pesquisa há outras coisas escritas que não interessam nessa etapa da atividade (explicação da tarefa aos pais).
- Pedir que as crianças ordenem as alturas para que descubram quem é o mais alto do seu grupo de entrevistados. Durante a atividade, auxiliarei os grupos no processo de ordenação, questionando-os sobre os critérios utilizados para decidir qual é o número maior.
- Cada grupo levará para a roda o papel com o nome e a altura da pessoa mais alta que encontraram.
- Em roda, as crianças terão que descobrir quem é o mais alto de todos (ordenar). Os números estarão no meio da roda, de maneira que todos possam visualizá-los.
- Novamente irei questionálos sobre os critérios que usaram para ordenar os números.
- Depois, colocarei o papel com o nome e a altura da pessoa mais alta no cartaz que está no mural, já com o nome do mais alto da sala e o mais alto da creche.
- Ao final da atividade, explicarei às crianças que esse nome poderá ser substituído, desde que alguém encontre uma outra pessoa mais alta do que a que já está ali.
Projeto Os Mais Mais5
Destinatários
Crianças da pré-escola (6 a 7 anos)
Professora Responsável
Fabiane Aparecida Rodrigues
Formadora
Priscila Monteiro
Objetivo
Espera-se que com esse projeto as crianças reflitam sobre as regras de organização do nosso sistema de numeração, colocando em jogo suas hipóteses, confrontando com a de seus colegas, estabelecendo critérios de comparação de escritas numéricas.
Conteúdo
Comparação e ordenação de escritas numéricas isoladas.
Objetivo compartilhado com as crianças
Montar um livro dos “mais mais” (livro dos recordes).
Etapas previstas
1ª atividade:
A professora seleciona e leva para a roda materiais do tipo livro dos recordes (Guinness Book, livro de curiosidades, etc.). Faz circular o material entre as crianças, lendo algumas das curiosidades. Em seguida, propõe ao grupo a elaboração de um “livro dos mais mais”, com informações coletadas por eles.
2ª atividade:
Novamente em roda, a professora combina com o grupo o tipo de informação que irão coletar: idade, altura, número de sapato, peso, número de filhos, etc. As crianças vão fazendo as sugestões e a professora vai anotando na lousa ou num cartaz.
3ª atividade:
A professora organiza uma pesquisa com as crianças sobre a altura de cada um. Mede as crianças com o auxílio de uma fita métrica e anota a altura de cada um num pedaço pequeno de papel. Em outro momento, em grupos de 4, as crianças comparam suas alturas e decidem quem é o mais alto. A professora circula entre os grupos observando e questionando como fizeram para decidir qual é o maior. Quando o grupo chegar a um consenso a professora recolhe o papel com o número selecionado.
4ª atividade:
No dia seguinte, a professora confecciona um cartaz para organizar os dados obtidos por todos os grupos. Cada grupo mostra o seu número – é aconselhável expor os números em local onde todos possam ver – e todos discutem e decidem qual é o maior. Colocam no cartaz o papel com o maior número encontrado.
5ª atividade:
A professora propõe ao grupo que descubram qual é a pessoa mais alta da escola. Para isso, organiza uma pesquisa em que as crianças, divididas em grupos de 4, em horários alternados, saem da sala, munidas com uma prancheta, papel e lápis para entrevistar as pessoas da escola, perguntando sua altura – combina-se previamente quem cada grupo irá entrevistar.
De volta à sala, cada grupo se reúne e decide qual é o maior número encontrado. Novamente a professora circula entre os grupos observando e questionando como fizeram para decidir qual é o maior. Segue o procedimento da etapa anterior, confeccionando-se outro cartaz.
6a atividade:
A professora propõe que as crianças pesquisem em suas casas se alguém conhece uma pessoa mais alta do que a encontrada na escola. Para isso, as crianças levam para casa um papel anotado com a altura da pessoa mais alta da escola. Escrevem nessa mesma folha, se preciso com ajuda de um adulto, a maior altura que conseguiram descobrir.
De volta à escola, as crianças se reúnem em grupos e decidem qual é o maior número dentre aqueles coletados. Novamente a professora organiza um cartaz, que pode ser grudado com velcro ou outro recurso como o quadro de pregas, para que possa trocar se as crianças, mais tarde, encontrarem um número maior.

Ficha técnica
Esses procedimentos se repetem para cada informação selecionada: idade, número do calçado, e outras. As crianças podem fazer entrevistas no bairro, pesquisar na internet, em livros, etc. Ao longo do projeto, as crianças podem trazer novos números referentes aos itens já pesquisados, se considerarem que este é maior do que o já encontrado.
Quando todos os dados numéricos estiverem organizados nos cartazes expostos na sala, a professora organiza o livro junto com seus alunos. Cada criança pode confeccionar seu próprio livro a partir das informações coletadas pelo grupo. A cada dia a professora entrega uma página para as crianças colocarem uma das informações (copiam dos cartazes) e fazerem sua ilustração. No final, organizam as páginas, o índice e a introdução.
5 Projeto elaborado durante o curso de Matemática promovido pela AME.
Realização: Centro de Formação de Professores Casa do Aprender – Associação das Mulheres pela Educação (AME)
Curso: Aprendizagem e Ensino da Matemática na Educação Infantil Tel.: (11) 3603-5536. E-mail: ame_casadoaprender@ig.com.br
Professora: Priscila Monteiro
Locais em que os projetos aconteceram: Creche Casa do Aprender – Rua: Piacatú, 2058 – Jardim Munhoz Osasco – SP. CEP: 06240-160 Tel.: (11) 3696-8354. E-mail: casadoaprende@hotmail.com
Equipe Gerente: Irene Longhi
Coordenadora pedagógica: Maria da Guia Vieira Batista
Educadora: Fabiane Aparecida Rodrigues
Centro Presbiteriano Humanitário de Ação Social (Cephas)
Centro Presbiteriano de Educação Infantil – Av. Amazonas 1.255 – Cohab II – Carapicuíba – São Paulo – SP. CEP: 06327-270 – Tel.: (11) 4187-6217
Equipe Diretora: Solange Gonçalves Mendonça Moreira
Coordenadora pedagógica: Josilda Gomes de Amorim Souza
Educadora: Gláucia Fischer Vicente
Para saber mais
- Didática da Matemática: Reflexões Psicopedagógicas, de Cecília Parra Irmã Saiz e organizadoras. Ed. Artes Médicas. Tel.: (11) 221-9033. Edição esgotada. Encontrado em bibliotecas e sebos
- O Homem que Calculava, de Malba Tahan. Ed. Record. Tel.: (11) 3331-6766
Sites:
- www.somatematica.com.br
- http://www.terra.com.br/matematica
- www.livrariacultura.com.br – entrar no Cultura News, março/05. Há uma ótima entrevista com o professor de Matemática Antonio José Lopes, conhecido como Bigode
Agradecimento especial a Cláudia Rocha (educadora de CEI na cidade de São Paulo, que colaborou no registro do projeto), pelo registro minucioso durante a apresentação deste trabalho.


