GIULIANNY RUSSO E MIRUNA GENOINO²
REFLETINDO SOBRE AS DIFERENTES FORMAS DE REGISTRAR, OS PROFESSORES DESCOBREM
MUI TO SOBRE SEUS ALUNOS E SUAS FORMAS DE PENSAR.
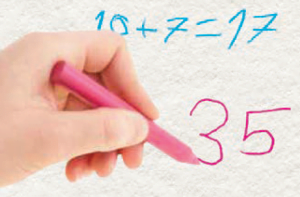
Quais situações didáticas podem mobilizar crianças do 1º ano a lançar mão do registro escrito quando deparadas com uma situação problema? Os alunos do 1º ano são capazes de refletir sobre suas formas de registrar? Que estratégias eles utilizam para colocar em jogo seus saberes quando são convidados a resolver problemas? Que maneiras encontram para registrar? E de que forma o professor pode promover a reflexão sobre essas estratégias?
Procurando respostas para essas indagações, promovemos diversas situações nas quais os alunos tivessem de resolver problemas do campo aditivo, registrando, cada qual do seu jeito, os meios para chegar às conclusões, vivenciando, depois, momentos de trocas mediadas pelo professor para se discutir estratégias. Essas são as situações analisadas que deram origem às reflexões aqui apresentadas.
1 A motivação para investigar esse tema partiu da definição do objeto de estudo do Simpósio Interno da Escola da Vila, em 2012, que
centrou-se em reflexões sobre a escrita. Este texto foi publicado na íntegra, em 2013, na revista Conversa de Professor, no 2, do
Centro de Formação da Escola da Vila.
2 Professoras do 1o ano da Escola da Vila. Especialistas em alfabetização e mestrandas na Universidad Nacional de La Plata, Argentina, no programa Escritura y Alfabetización, dirigido por Mirta Castedo.
Por que a escolha de trabalhar com as situações problemas?
Segundo Roland Charnay³, o conhecimento matemático origina-se de situações problemas – um obstáculo a ser superado – e, por isso, atividades que envolvam a resolução de problemas são fundamentais para a atribuição de sentido aos conceitos matemáticos. Os problemas oferecem um contexto concreto sobre o qual a criança pode refletir e mobilizar todas as estratégias de que dispõe para responder ao que lhe é solicitado, articulando, assim, seus conhecimentos anteriores aos obstáculos, limites e desafios que cada nova situação impõe.
Em geral, não oferecemos nenhum modelo, método ou fórmula de resolução. Ao terem de lidar com uma situação problema, os alunos precisam colocar em jogo tudo o que sabem e, dentro de um mesmo grupo, podem surgir variadas estratégias para solucioná-la. Essa diversidade é um potente objeto de trabalho, pois favorece a análise e a reflexão de diferentes respostas e procedimentos quando comparados e confrontados, o que reafirma a importância deste tipo de ação.

“É principalmente através da resolução de uma série de problemas escolhidos pelo professor que o aluno constrói seu saber, em interação com os outros alunos. A resolução de problemas (e não de simples exercícios) intervem assim desde o começo da aprendizagem4.” De fato, os alunos têm a oportunidade de, ao elaborar uma resposta, explicar o que pensaram, evidenciando-se, assim, os aspectos que levaram em consideração e como os articularam. Dessa forma, tornam-se conscientes de seus saberes, os reconhecem e apropriam-se deles. Optamos, com base nesses pressupostos, por apresentar problemas que trabalhassem com o campo aditivo (adição e subtração) e envolvessem números de um e dois algarismos.
Consideramos, também, que seria interessante trabalhar com problemas que permitissem, dentro das possibilidades da faixa etária, trabalhada uma variedade de estratégias quanto à resolução: palitinhos, contagem nos dedos, decomposição e até mesmo o cálculo mental – para gerar problematizações no momento da discussão.
Os dois primeiros problemas propostos foram:
Lucas e Théo têm, juntos, uma coleção de 15 carrinhos. Ganharam 5 de sua mãe. Quantos carrinhos
eles têm agora?
Luma tem em sua casa 27 bichinhos de pelúcia. Foi dormir na casa de sua amiga ana, levando 7 deles. Quantos bichinhos de pelúcia sobraram em sua casa?
O que pudemos observar quanto aos problemas em si foi que os alunos não demonstraram dificuldade em compreender o que estava sendo apresentado pelo enunciado e rapidamente começaram a resolver os problemas, sem, porém, utilizar o registro escrito. A maioria das crianças fez contagens utilizando os dedos das mãos ou anotou um número como resposta, não sendo, depois, capaz de recuperar o que efetivamente tinha realizado. Os poucos registros que apareceram decorreram do uso dos “palitinhos”, marcas para representar as quantidades indicadas no problema. Vale ressaltar que, em todos esses casos, encontramos os mais diversos resultados.
3 Em texto Aprendendo (com) a resolução de problemas. In: Didática da matemática: reflexões psicopedagógicas, de C. Parra. Porto
Alegre: Artes Médicas, 1996, p. 36-47.
4 Idem.
Levamos esse dado para ser discutido com a equipe pedagógica da série e comprovamos que esse comportamento se repetia nas demais salas, o que nos levou a refletir se os alunos de 1º ano seriam capazes de fazer o registro que gostaríamos e, nesse caso, por que faríamos essa solicitação por anotações.
De todo modo, o encaminhamento seguinte consistiu em pedir às crianças que nos explicassem oralmente ou por escrito como haviam feito para chegar àquele resultado. Foi comum ouvirmos
respostas como: “Deu 20”, “Como eu fiz? Eu contei”, “Como eu contei? Contando, oras!”, “Eu respondi 20, porque eu sei que é 20”. Essas respostas denotavam certo estranhamento ou falta de familiaridade com a nossa solicitação por anotações e, por isso, foram necessárias muitas ajudas no sentido de fazê-los compreender o que estávamos pedindo e também que registrassem no papel o que haviam feito para responder à questão. No momento seguinte, a maioria colocou “legendas” para relatar a ação: “Contei nos dedos”, “Fui contando assim 1, 2, 3, 4…”, “Fui contando” etc. Ainda que esses registros fossem
meramente comunicativos, ou seja, com os alunos anotando para atender à solicitação das professoras, a ação significava um avanço.
Esses primeiros registros foram importantes, sobretudo porque a dificuldade mostrada pelos alunos nos indicou que utilizar as anotações como apoio era um procedimento que precisava, ainda, ser foco de ensino e reflexão. O exercício indicava que, espontaneamente, as crianças não pensavam nos registros como um recurso importante para lidar com as situações problemas.
Diferenças com o ensino tradicional
A solicitação para que a criança registre como procedeu para solucionar um problema não é exatamente uma novidade no campo da Matemática. Contudo, tradicionalmente, essa comanda objetivava o treinamento e a utilização da “conta armada” – uma fórmula ensinada aos alunos antes mesmo que tivessem compreendido as transformações ocorridas – como única estratégia de cálculo válida: sobe 1 para a dezena quando a somatória das unidades é maior que 10, empresta 1 (que representa 1 dezena) para a unidade, na realização de uma subtração.
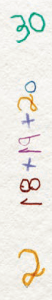
Nossa intenção, no entanto, ao contrário do ensino clássico da Matemática, era validar as diferentes formas de resolução, ampliando assim as possibilidades de estratégias, para que cada um avançasse na direção dos procedimentos “expertos” (aqueles mais rápidos, econômicos e eficientes). Ao solicitarmos que anotassem no papel o quê haviam pensado e como fizeram para resolver os problemas, partíamos do pressuposto de que fazer anotações seria uma ferramenta importante nesse processo. Apesar do desafio, é fundamental investir no registro escrito, já que, ao refletir sobre ele, cada criança se torna mais consciente de seus próprios saberes; além de que, ao compartilhar conhecimento com os demais, podem se consolidar e se generalizar em outras situações.
A partir disso, um próximo passo foi organizar situações de discussão a respeito dos problemas da escrita em Matemática. Ou seja, pautamos a elaboração dos problemas não apenas na ação de resolvê-los, mas também na reflexão sobre o que havia sido feito. Esse encaminhamento partiu do pressuposto de que: “Los intercambios, las explicaciones, las protestas de los alumnos, así como el recurso a la imitación de lo que hacen sus compañeros son un factor de progreso para los alumnos. El pensamiento de cada uno se construye en la confrontación con los demás5.”
Essa proposta didática se sustenta em dois princípios: primeiro, o da resolução de problemas como algo que desafia as estruturas do sujeito, mobilizando-o a acionar todos os conhecimentos prévios de que dispõe na tentativa de articular os dados do problema a fim de responder à questão; e depois, o princípio
da discussão, em que, por meio de habilidades comunicativas, os sujeitos confrontam seus procedimentos, agregando novas informações e gerando novos desequilíbrios sempre que um novo dado não se encaixa nos esquemas anteriores (assimilação), levando à construção de novos saberes à medida que são feitos esforços adaptativo de acomodação6.
Portanto, não basta fazer (resolver o problema) para aprender: é preciso refletir sobre o que foi realizado.
5 Los niños, los maestros y los números. Desarrollo curricular, de Cecilia Parra e Irma Saiz. Buenos Aires: Governo da cidade de
Buenos Aires, 1996, p. 22. Tradução livre das autoras: “As trocas, as explicações, as manifestações dos alunos, assim como o recurso
à imitação do que fazem seus colegas são fatores de progresso. O pensamento de cada um se constrói na confrontação com os
demais”.
6 Seis estudos de psicologia (1968), de Jean Piaget. Rio de Janeiro: Forense Universitária, 2003. Piaget define como processo
de equilibração o esforço adaptativo de assimilação e acomodação. Segundo o autor, o que impulsiona o sujeito a atuar sobre o
mundo, tentando desvendá-lo, é a necessidade de equilibração: ele assimila aquilo que vem de fora e gera um desconforto, porque
não pertence às suas estruturas anteriores e, no esforço de livrar-se desse desconforto, ele acomoda o que foi assimilado aos seus
esquemas. Desse modo, se apropria de maneira única de um conhecimento inicialmente externo a ele.
As discussões
As primeiras discussões foram pautadas por uma mediação bastante clara entre os saberes de cada um, realizada pelas professoras de sala.
Vejamos trecho de uma delas:
Problema: Lucas e Théo têm, juntos, uma coleção de 15 carrinhos. Ganharam 5 de sua
mãe. Quantos carrinhos eles têm agora?
Aluno 1: coloquei os pauzinhos (15), para eu juntar tudo. E depois eu fiz mais esses pauzinhos (5). Aí, eu juntei tudo e deu 20. Era a minha técnica (sic).
Professora: por que 15 pauzinhos?
Aluno 2: para ele não esquecer. Ele marcou o 5 que é que ele ganhou (sic).
Aluno 3: o 15 é o que eles tinham antes (sic).
Professora: todos resolveram como o aluno 1?
Aluno 4: eu pensei o mesmo que o João, só que na cabeça. Primeiro fiquei com o 15 na cabeça e depois juntei o 5 (sic).
Aluno 5: eu contei cinco na minha mão e guardei o 15 na cabeça. Depois eu somei com o 5 da mão. Eu fiz assim [ mostrando nos dedos ] 1, 2, … , 15 (sic).
Aluno 6: eu contei 16, 17, 18, 19, 20. Eu já sabia que 5 + 5 é 10 e 5 + 5 + 5 são 15 e que 10 + 10 é 20, daí se tiver quatro cincos, dá 20 (sic).
Aluno 7: eu juntei o 5 e o 15 (sic).
Aluno 3: eu contei do 15 mais 5 aí deu 20 (sic).
Aluno 8: eu fiz 15 palitinhos e depois 5 palitinhos, e depois contei tudo. Com as mãos não dá para fazer o 15, então se precisar pode fazer os palitinhos (sic).
Professora: e aí, como souberam a resposta?
Aluno 2: eu descobri que o 16, 17, 18, 19 começa com 1 e o depois vem o 20, que começa com 2. Então, se a gente soma o 5 no 15, aí é 20 (sic).
Todos os alunos envolvidos nessa situação, tendo apenas registrado o resultado final, tiveram que, durante a discussão, repensar os dados do problema e elaborar formas de explicar o seu pensamento. É possível perceber, pela transcrição acima, o quanto conversar sobre o problema permitiu que os alunos levantassem uma série de possibilidades para a resolução de um cálculo aparentemente simples (15 + 5), mas que mobilizou variados saberes.

Algumas crianças ainda se mostraram confiantes com o recurso dos dedos, mas outras arriscaram experimentar o registro escrito como possibilidade de dar conta da situação. É importante notar como a situação de discussão permitiu que um aluno conseguisse “traduzir” a contagem nas mãos para o registro escrito quando afirmou que, por ter apenas dez dedos, seria interessante acionar o recurso das marcas gráficas dos “palitinhos”.
Ainda analisando a situação de discussão, vale ressaltar, por exemplo, que o aluno 6 apresentou uma ideia bastante refinada para a faixa etária – utilização de cálculos mentais (5 + 5 = 10) para apoiar o cálculo necessário (de 15 + 5) –, embora fosse uma criança com dificuldades não só para registrar, mas também para explicar como havia feito para chegar à resolução do problema. Contudo, ao ouvir os colegas, o aluno foi capaz de dar uma explicação bastante interessante do ponto de vista das estratégias em jogo.
Para esse aluno, que realizava o cálculo mental de maneira muito eficiente, a importância de registrar residiu em, de certa forma, se apropriar dos procedimentos que ele realizava, sem necessariamente se dar conta deles. Além disso, o registro lhe oferecia a possibilidade de conferir o resultado obtido e localizar a ocorrência de erros.
Esse caso exemplifica como as situações de discussão podem ocorrer em momentos que “provoquem a elaboração e a colocação em funcionamento de conhecimentos implícitos; que possam explicitá-los, que os expressem em uma linguagem compreendida por todos”7.
As discussões permitem, dessa forma, que cada criança se torne consciente dos mecanismos que utilizou na resolução e que, ao mesmo tempo, ofereça aos colegas contribuições para que eles possam resolver outras situações problema.
Nas duas classes em que a proposta ocorreu, algo nos chamou a atenção: ainda que os alunos tivessem usado pouco ou nenhum registro gráfico na discussão dos dois problemas, as crianças foram capazes de mobilizar uma variedade bastante grande de recursos para resolver o exercício apresentado. As diferentes estratégias, ao serem explicitadas pelos alunos, foram transcritas na lousa pela professora, como podemos ver na imagem abaixo relacionada à retomada do problema 2 (Luma tem em sua casa 27 bichinhos de pelúcia. Foi dormir na casa de sua amiga Ana, levando 7 deles. Quantos bichinhos de pelúcia sobraram em sua casa?):
7 A motivação para investigar esse tema partiu da definição do objeto de estudo do Simpósio Interno da Escola da Vila, em 2012, que
centrou-se em reflexões sobre a escrita. Este texto foi publicado na íntegra, em 2013, na revista Conversa de Professor, no 2, do
Centro de Formação da Escola da Vila.
O próximo passo foi apresentar aos alunos os seguintes problemas:
Num jogo de trilha:
1. Nina estava na casa 29 e tirou 6 pontos nos dados. Em que casa ela foi parar?
2. Rafaela estava na casa 15 e tirou 6 em um dado e 5 no outro. Em que casa foi parar?
3. Luciano estava na casa 28. Tirou 5 em um dado e 5 no outro. Em que casa foi parar?


Além dos conhecidos “palitinhos”, apareceram registros nos quais as marcas vinham com indícios de controle de contagem (quando os alunos fazem os risquinhos e depois colocam novo risco em cima dos mesmos, no momento de contar o total) e outros (exemplo 1) em que o aluno conservava uma das parcelas e utilizava marcas apenas para o número que gostaria de adicionar ao número indicado (sobrecontagem). Em alguns casos (exemplo 2), foi utilizado o próprio número no lugar dos risquinhos. Além desses exemplos, algumas crianças mostraram indicações de conseguir usar, no caso do problema 3, o cálculo mental de 5 + 5 para efetuar a adição.
Nessa proposta, escolhemos problemas que demandassem a realização de cálculos parciais para se chegar ao resultado final, de forma que os alunos pudessem, talvez, sentir a necessidade de utilizar o registro escrito para dar conta da nova situação. Os problemas foram, ainda, resolvidos, majoritariamente, como da primeira vez: de cabeça ou usando os dedos, apresentando apenas o resultado final. No entanto, apareceram novos registros, com escritas matemáticas que até então não haviam surgido em outras situações.
Ainda que o avanço estivesse claro, era essencial continuar investindo na discussão sobre o registro, já que a maioria dos alunos das duas classes ainda indicava apenas um número como resposta, fosse ela correta ou não. Assim, elaboramos outro encaminhamento: pedimos aos alunos que socializassem, em pequenos grupos, suas formas de resolver os problemas, tendo que registrar qual acreditavam ser o resultado final, bem como uma boa forma de justificar essa escolha.
A atividade se mostrou bastante importante para o trabalho dos alunos, já que ao conversarem em pequenos grupos, passaram a registrar no papel o melhor procedimento para que fosse possível compreender, ajudar o outro a entender seu pensamento, posicionar-se, colocar-se.
Com essa proposta percebemos que os alunos começavam a olhar para a escrita em Matemática não como uma obrigação, mas como um recurso potente para solucionar os problemas apresentados.
Após o trabalho em pequenos grupos, encaminhamos uma discussão coletiva na qual, diferentemente
das primeiras conversas, um maior número de alunos se posicionou e expôs seus pontos de vista, ampliando consideravelmente a variedade das formas de registro.
A partir dessa discussão, outro aspecto que mobilizou os alunos foi a questão do “certo e errado”; muitos mostraram preocupação em entender qual seria a solução correta, a partir dos registros escritos feitos coletivamente. Ou seja, quando identificavam uma solução que não era correta, conseguiam justificar pelo registro (“Você precisava fazer 29 pauzinhos, você fez só 27!”), assim como, para explicar uma solução correta, também se apoiavam na escrita (“Este jeito está certo porque… olha [fazendo marcas na lousa], 5 + 6 são 11, e aí junto com o 15 e ficam 26!”). Desse modo, os alunos começaram a desenvolver
as explicações e os argumentos que justificavam suas ações e pensamentos.
Ainda que nossa meta não se limitasse ao alcance do resultado correto, acreditamos ter sido importante que nossas turmas de 1o ano passassem a ter essa preocupação, já que o registro escrito oferece possibilidades mais evidentes, porque concretas, para localizar erros e visualizar outras articulações entre os números. Observamos, inclusive, que os alunos começavam a se distanciar do registro como tarefa, passando a usá-lo como recurso.
Registrar em parceria: o encaminhamento final
Após essas ricas atividades vivenciadas pelos alunos, elaboramos um encaminhamento que nos permitisse avaliar o percurso feito por eles e os avanços conseguidos. Apresentamos ao grupo três problemas para serem resolvidos em duplas, com apenas uma folha para registrar:
1. As crianças da educação infantil farão um lanche coletivo. As professoras pediram 5 caixas de suco de maracujá, 5 de uva e 7 de maçã. Quantas caixas de suco terão ao todo?
2. Uma das professoras achou que seria pouco suco e solicitou outras 4 caixas. Quantas caixas de suco terão no lanche?
3. No dia, o entregador esqueceu-se de levar 6 caixas. Quantas caixas de suco tiveram no lanche?
Na elaboração dos problemas, organizamos uma sequência em que, para avançar, os alunos tiveram de considerar o resultado do problema anterior. Orientamos que, trabalhando em duplas e contando apenas com uma folha de papel, cada um deveria, a princípio, mostrar e explicar ao outro como resolver o problema. Então, em um segundo momento, as crianças deveriam decidir a forma mais eficiente e econômica de registro. Definimos as parcerias de acordo com o procedimento de resolução de cada criança, buscando formar duplas que possuíam estratégias distintas. Portanto, para realizarem a proposta, os alunos tinham de observar, discutir, conversar, argumentar, escutar, ponderar e concluir.
Durante a atividade, pudemos observar que os alunos conversavam não apenas sobre o que o problema solicitava, mas na melhor forma de organizar a escrita matemática de modo a chegar à resposta final.
Como resultado dessa proposta, tivemos a totalidade de duplas das duas salas de 1o ano colocando em jogo registros escritos variados, sem que nenhum aluno realizasse a anotação como na primeira situação, escrevendo algo apenas para informar o que tinham feito.
Dessa forma, apareceram diversos “(…) procedimentos nos quais as anotações são um apoio necessário para o desenvolvimento do procedimento”8, como é o caso de marcas gráficas (palitinhos, risquinhos etc.), que são “útiles y encierto sentido necesarias para sus autores porque funcionan como sostén sobre el cual efectúan el conteo. Son un testimonio de su procedimiento pero también un medio – y en algunos
casos, por cierto bien eficaz – para desplegarlo sin recurrir al material concreto”9.
Atualmente, algumas dessas marcas já aparecem com registros mais sofisticados, como o uso de números, por exemplo, para o controle dos “palitinhos”, assim como o registro de cálculos colocados em jogo na resolução:

Outros registros mostravam “produções nas quais a escrita pode ou não ser necessária, mas funciona principalmente como um meio de controle”10, que são os registros escritos em que os alunos “ya emplean procedimientos de cálculo y logran aproximarse a la formulación aritmética de los mismos, la escritura de las descomposiciones decimales puede o no ser una necesidad para obtener el resultado, depende de la magnitud de los números y del dominio de los alumnos sobre ellos. Pero la escritura que realizan les permite controlar tanto las descomposiciones decimales como los cálculos parciales que realizan”11.
Dois exemplos indicam como muitas crianças utilizaram esse tipo de procedimento. Alguns alunos realmente usavam a formulação aritmética para controlar os dados do problema e assim chegar à resposta:

Outros alunos, claramente, indicavam que ainda usavam o recurso dos dedos para os cálculos, mas que conseguiam elaborar formulações aritméticas para controlar os cálculos e indicá-los no papel:

8Idem, p. 8.
9 Idem, p.9. Tradução livre das autoras: “(…) úteis e, em certo sentido, necessárias para seus autores (as crianças) porque funcionam
como apoio sobre o qual efetuam a contagem. São testemunhos de seu procedimento, mas também um meio – e, em alguns casos,
com certeza, bem efi caz – para colocá-los em jogo sem recorrer ao material concreto”.
10Idem, p. 8.
11 Idem, p.10. Tradução livre das autoras: “(…) já utilizam procedimentos de cálculo e conseguem aproximar-se da formulação
aritmética dos mesmos; a escrita das decomposições decimais pode ou não ser uma necessidade para obter o resultado, depende
da magnitude dos números e do domínio dos alunos sobre eles. Mas a escrita que realizam lhes permite controlar tanto as
decomposições decimais como os cálculos parciais que realizam”.
Comparando essa situação final com os registros observados no primeiro problema trabalhado, pudemos verificar que os alunos das duas classes de 1o ano passaram a mobilizar diferentes recursos e estratégias com relação ao registro escrito em Matemática, ação que os ajudou a pensar e a decidir sobre as melhores formas de resolver os problemas apresentados em sala de aula.
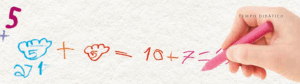
Considerações finais
Ainda que este artigo apresente o resultado de apenas um semestre de trabalho, acreditamos que alguns elementos analisados em nossa investigação possam ser bastante importantes para validar e pensar o trabalho com situações problemas com alunos do 1o ano do Ensino Fundamental.
Em primeiro lugar, embora sejam alunos em processo inicial de construção de saber envolvidos na resolução de problemas, a organização de situações criteriosamente planejadas mostrou o quanto esse tipo de proposta pode oferecer enorme gama de possibilidades aos alunos no sentido de colocar em jogo seus saberes matemáticos e, ao mesmo tempo, participar de momentos privilegiados de troca de informações e questionamentos com seus colegas de sala.
Essas situações de socialização entre os alunos se configuraram como uma importante estratégia didática para investir nos registros escritos durante a resolução de um problema.
Desta forma, nossa pergunta inicial sobre quais situações didáticas seriam potentes para as crianças pensarem, utilizarem e avançarem no registro escrito do procedimento de resolução – e que partia do pressuposto de que registrar é importante, uma vez que permite à criança avanço em seus conhecimentos matemáticos – encontrou boas respostas no desenvolvimento das situações relatadas. Como destaca Wolman: “En efecto, las anotaciones que los niños realizan permiten que los modos de resolver se exterioricen, se objetiven (expresión privada, independiente de su comunicación) permitiendo a los alumnos pensar sobre sus conocimientos. La explicitación del modo de resolución, en este caso por escrito, los ayuda en el proceso de toma de conciencia de los procedimientos que emplean”12.
Ou seja, apenas colocá-los diante dos problemas não foi, em nenhum caso, suficiente para que pudessem avançar em seus registros escritos, que foram ganhando variedade e complexidade na medida em que as discussões aconteceram e as classes puderam refletir, com a mediação do professor, sobre as variáveis dos problemas, estratégias adequadas e sobre outras coisas a partir dos erros, dos resultados alcançados
e do estabelecimento desses registros.
A reflexão sobre a ação, conduzida coletivamente, fez com que os alunos pudessem ressignificar também os registros que produziam, uma vez que passaram a assumir outra função importante: a de comunicar aos colegas a forma como os problemas tinham sido resolvidos.
A proposição dessa variedade de situações permitiu também que chegássemos a algumas observações sobre os registros escritos, a serem consideradas no momento de realizar diferentes intervenções com os alunos. Percebemos, por exemplo, que muitas crianças do 1o ano usavam com maior frequência o registro escrito como apoio necessário quando a resolução do problema envolvia a ideia da subtração, e de maneira ainda mais frequente, colocavam em jogo registros escritos mais voltados à comunicação da
ação quando a ideia envolvida era a da adição. Levantamos algumas hipóteses explicativas para isso. Uma delas diz respeito ao fato de que as crianças, geralmente, têm menos experiências com as noções de subtração. Também consideramos que a récita numérica pode influenciar nesse processo, já que a recitação é trabalhada mais sistematicamente na ordem crescente e que sua “fluência” facilita o cálculo, sobretudo quando se apoia na contagem.
Vale dizer que processo semelhante pôde ser verificado em algumas situações pontuais oferecidas recentemente no campo multiplicativo: com os alunos necessitando muito mais do registro escrito para a ideia da divisão do que para a ideia da multiplicação, aspectos que poderiam ser desdobrados em possíveis novas investigações. Finalmente, uma consideração que nos parece essencial é a de validar a resolução de problemas no 1o ano como uma situação didática que efetivamente oferece muitas possibilidades de desenvolvimento e discussão, mesmo com alunos que estão iniciando o Ensino Fundamental. Ainda que seja uma experiência inicial desse tipo de proposta, foi possível perceber o quanto encaminhamentos precisos, durante a elaboração dos problemas (variáveis numéricas, enunciados etc.), no decorrer da resolução (individualmente, em dupla, em grupos, usando um papel, compartilhando a folha etc.) e após a solução (discutindo com a dupla, analisando em grupo, discutindo
em meio grupo, coletivamente etc.), são potentes estratégias didáticas que permitem aos alunos avançar muito no que diz respeito a alguns conteúdos essenciais no currículo de Matemática das séries iniciais.
Torna-se então necessário e produtivo seguir investindo e investigando as intervenções mais eficientes, de maneira a ampliar ainda mais as possibilidades de trabalho com os procedimentos de registro na resolução de problemas matemáticos em classes do 1º ano do Ensino Fundamental.


